Labels
Toggle on/off for simulation and select for dependence tests.
Off
On
Selected
Stmt
S1
S1
none
Write
A(I)
A(I)
A(I)
Read
A(I)
A(I)
A(I)
They are all toggled ON by default and selection is available when analyzing subscripts.
or Run automatically
Dependencies:
RAW
WAR
WAW
Mixed
Note: these are iteration vectors (see below), not array calls/references!

Dependence

There are 3 types of data dependence; consider, in a piece of code, two statements S1 and S2 that execute in order:

Flow (True) RAW hazard

S1 a = ..

S2 .. = a

Denoted S2 δ S1

Anti WAR hazard

S1 .. = a

S2 a = ..

Denoted S2 δ-1 S1

Output WAW hazard

S1 a = ..

S2 a = ..

Denoted S2 δ0 S1

Only data flow dependences are true dependences. Anti and output can be removed by renaming.

Iteration Space

Now that we have formalized dependence between two singular statements, let's look at it in terms of a loop or a block of nested loops that iterate over statements.

Each iteration in a loop has a iteration number which is the value of the loop index at that iteration.

Iteration vector I of iteration is the vector of integers containing numbers for loops in order of nesting level.

DO I=1,4
DO J=1,6
STATEMENT
ENDDO
ENDDO

Iteration vector (2,1) of S is when I = 2 and J = 1.
The iteration vectors are ordered by execution order.

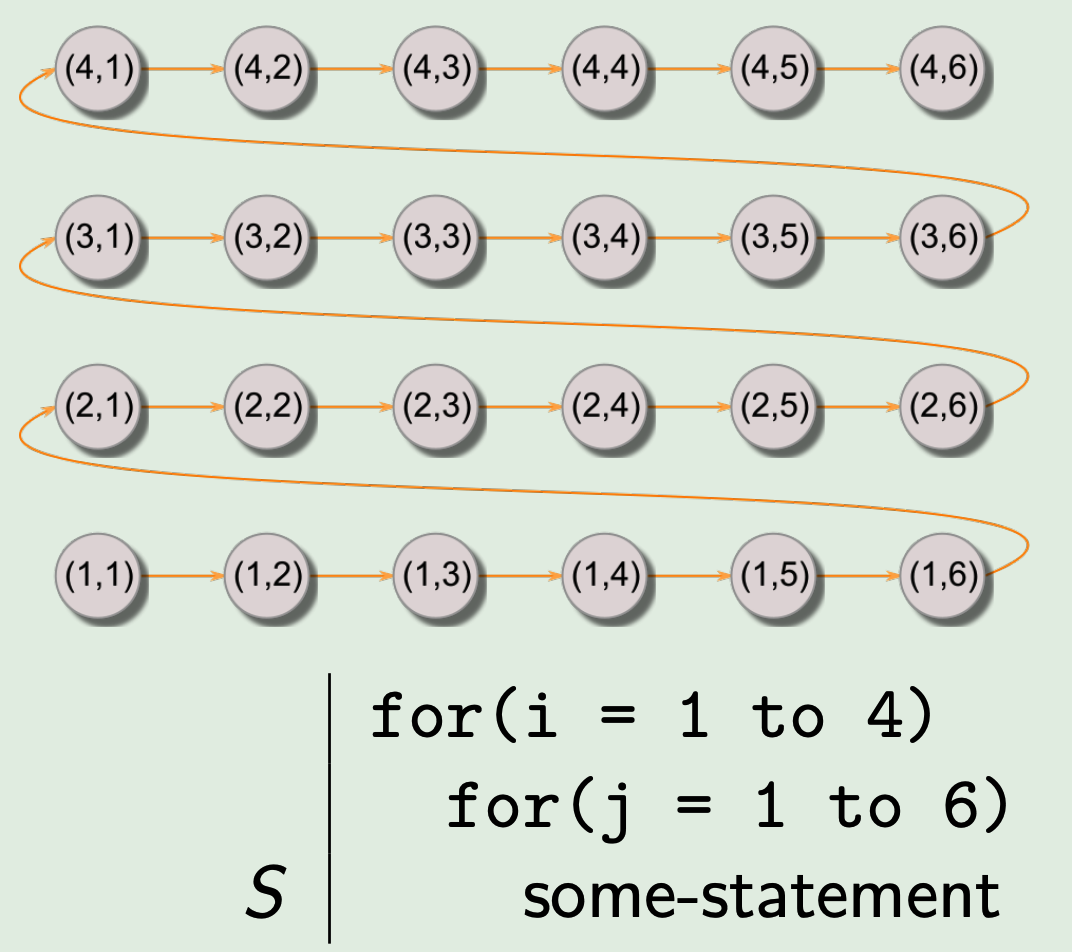
Our iteration space is the set of all iteration vectors in order of execution given a loop or a nested loop, where the nodes are the iteration vectors and the directed edges showcase dependence of an interation on another. If there is an edge from an iteration I to an interation J, that means that there is a statement in iteration J that depends on a statement in iteration I. There is also a distance between the iterations on the edge, which might be helpful to know in order to concretize the dependence and find a direction of the dependence in our loop.

Depending on the iteration in which two statements are executed, we can two types of loop-based dependencies:

Loop-independent dependency
If statement S2 depends on S1 and S1,S2 execute in the same iteration. Distance (0,0,..) and Direction (=,=,..).

Loop-carried dependency
If statement S2 depends on S1 and S1,S2 execute in different iterations.

Distance and Direction

Dependence distance
If dependence is between iteration Iwrite and Iread, then distance is Iread - Iwrite.
Example: Write A(10,11) at iteration (5,5). Read A(10,11) at iteration (5,6). Distance is (0,1).

If dependence distances all same, then say loop has that dependence distance. But, loop may have many different dependence distances.

Direction vector summarises directions. If first non = element is < then indicates flow dependence.

  • < - All +ve
  • > - All -ve
  • = - All 0
  • * - Mixed

For example, given distances:

  • (0, 1, -1, -1)
  • (0, 2, -2, 0)
  • (0, 3, -3, 1)

Direction is:

  • (=, <, >, *)

You can also check the Compiler Optimization course slides on the Iteration Space topic here.

Dependencies:
δ
RAW
δ⁻¹
WAR
δ⁰
WAW
δᵢ
subscript i denotes level of loop carried dependence
You can click on or move the statements around to better see the notation!

Dependency Graph

Rather than looking at the problem in terms of iterations, we can consider statements individually: on what other statements they depend and specify the type and the level of loop carried dependence. We can visualize the dependence in this delta graph regardless of the number of loop levels as we are not limited at 2. Here the nodes are the statements and the edges are the delta-notation of the dependencies.

Level of loop carried dependence
Level of loop carried dependence is the index of the left-most non = in direction vector. Written as subscript, e.g.

  • δ1 for (<, =, =)
  • δ-13 for (=, =, >)
  • Infinity for in same loop, e.g. δ∞ for (=, =, =)

Consider the following example:

DO I=1,5
DO J=1,5
A(I,J-1)=A(I,J)
A(I,J)=A(I-1,J-1)
ENDDO
ENDDO

Loop-carried:

  • A(I,J-1) and A(I,J) in S1 could have created a WAR dependence of distance (0,-1) and direction (=,>) => δ-12, but A(I,J) is overwritten in S2 - we don't include this in our dependence graph.
  • A(I,J-1) from S1 and A(I,J) from S2 create a WAW dependence of distance (0,1) and direction (=,<) => δ02
  • A(I,J-1) from S1 and A(I-1,J-1) from S2 create a RAW dependence of distance (1,0) and direction (<,0) => δ1
  • A(I,J) and A(I-1,J-1) from S2 create a RAW dependence of distance (1,1) and direction (<,<) => δ1

Loop-independent:

  • A(I,J) from both statements create a WAW of distance (0,0) and direction (=,=) => δ0∞

The resulting dependence graph is this:

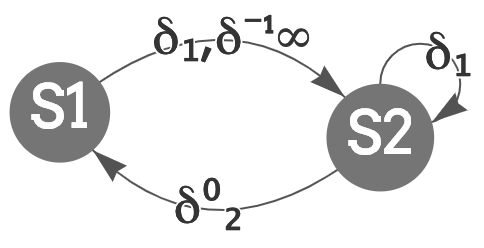
You can also check the Compiler Optimization course slides on the Dependence Graph topic here.

Array calls:
Subscripts:
Partitions:
This is quite different from iteration space and dependence graph sections. You get to capture subscripts, and analyze them step by step-first determing their type and then applying the corresponding test. You get the chance to think for yourself before advancing to the next step. Subscript tests are used to prove independence statically by analyzing the array calls, rather than exaustively building an interation space, which is more so for didactical purposes and inefficient in practice.
Select 2 array calls for which to analyze dependence.
For the purpose of these subscript tests, select either:
  • 2 writes (either which can potentially write to both),
  • 1 write (which can write after read) and 1 read (which can read after write).
Reading alone does not cause dependence, and analyzing more than 2 array calls is not possible. Note: even if a subscript test presented in this section yields independence, there could still be a write after write dependence of an array call on itself.